Р. Вишневский
Явление фазового перехода света
Установлено,
что вектор скорости света электрона смещен в фазовом пространстве относительно
вектора скорости света фотона. Описан процесс трансформации электрона в фотон в
GR-поле атома. Вычислено значение углового смещения
вектора скорости света в процессе фазового перехода.
Процессы
излучения и поглощения света в природе являются самыми распространенными, они
происходят на всех уровнях организации материи. В физике элементарных частиц
этим процессам соответствуют четыре понятия: акт элементарного излучения, акт
исчезновения элементарной частицы, акт элементарного поглощения и акт рождения
элементарной частицы. Более того, эти понятия связываются попарно: известны
явления аннигиляции пары (например, электрон-позитрон) и процессы рождения
пары. Однако объединить все четыре понятия в одно пока не удается.
Это не покажется
странным, если вспомнить, что с открытием закона сохранения энергии-массы,
некоторые физики своеобразно понимали дуализм света, предлагая ликвидировать
понятие массы с целью устранения «дублирования».
Между тем,
светодинамика утверждает: дуализм света состоит в том, что фотон и элементарная
частица являются двумя крайними состояниями одной и той же энергии света. Не
раскрывая сути понятия «энергия», светодинамика связывает эти два равноправных
состояния света с помощью фазового перехода.
Фазовый переход
света определяется как нестационарный процесс, в котором свет испытывает
трансформацию и переходит в другое свое крайнее состояние: фотон или частицу, в
зависимости от направления перехода. Этот процесс здесь называется явлением
прямого и обратного фазового перехода (ФП) света. Светодинамика устанавливает
однозначное соответствие между элементарной частицей и фотоном.
Непременным
условием для осуществления ФП света является наличие искривленного
пространства, т. н. фрактала, в котором происходит сворачивание в спираль
траектории движения микрочастицы или фотона. Подобное пространство возникает в GR-поле
возбужденного ядра атома. Здесь не поднимается вопрос о первопричине появления
в природе фракталов, но при рассмотрении процесса ФП света всегда
предполагается наличие искривленного пространства.
Известный и
уважаемый физик-экспериментатор в популярной книге, посвященной
«суперобъединению», задается вопросом: что произойдет со световой волной, если
ее вернуть в точку излучения? И приводит ответ физика-теоретика: эта световая
волна вернется к нам из бесконечности.
Светодинамика
предполагает другой исход подобного эксперимента: световая волна, стянутая в
точку, вновь превратится в частицу, из которой она и произошла. Данная статья
посвящена изложению упрощенного, в основном графического, описания явления ФП
света.
Трудность этого
описания состоит не только в сложности самого описываемого процесса, но и в
отсутствии некоторых понятий, без которых описание невозможно. Например, в
физике отсутствует понятие комплексной массы микрочастицы. Существуют понятия
античастицы, дырки, эффективной массы, заряда, есть даже понятие комплексной
амплитуды вероятности. Но масса понимается в смысле, как ее определил Ньютон –
инертная.
Межу тем,
микрочастица может быть описана с помощью комплексной массы1), действительную часть
которой составляет ее гравитационная масса (mG), а мнимая часть
представлена ротационной массой (mR). Для электрона:
me = mG – imR.
Это
влечет за собой понятие потенциала микрочастицы:
сe2 = V02 + Vsp2,
где V0 – орбитальная
(гравитационная) скорость электрона, Vsp спиновая
(ротационная) скорость, сe – вектор скорости света в
пространстве электрона.
Треугольник
скоростей электрона. Указание на параметры треугольника скоростей электрона дает т. н.
постоянная тонкой структуры:
α = 0,0072973506.
Физический смысл этой
постоянной обнаруживается после несложных преобразований выражения для радиуса
боровского первого а0, которое содержит эту постоянную:
 .
.
Другая постоянная Ридберга, ![]() , выражается через частоту обращения электрона вокруг ядра
атома водорода так:
, выражается через частоту обращения электрона вокруг ядра
атома водорода так:
 ,
,
а сама частота
обращения может быть представлена в
виде:
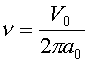 ,
,
где V0
– скорость
движения электрона вдоль боровской орбиты. Несложная подстановка позволяет
получить значение постоянной тонкой структуры:
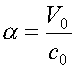 . (1)
. (1)
Оно указывает на треугольник
скоростей электрона, однако оставляет неопределенность: является ли скорость
света с0 гипотенузой треугольника или его катетом?
Для выяснения
поставленного вопроса следует обратиться к выражению комптоновского радиуса
электрона rk:
![]() ,
(2)
,
(2)
где r0 – радиус орбиты электрона, re
–
классический радиус. Таким образом, rk есть среднее геометрическое между r0
и re. Три радиуса электрона
образуют прогрессию, знаменателем которой служит постоянная α.
На рис. 1 приведено построение, из которого находится среднее геометрическое rk. Очевидно, что знаменатель прогрессии здесь равен:
![]() .
.
Сопоставляя это
равенство с (1), легко определить треугольник скоростей электрона, что и
отражено на рис. 2. Угол δ –
внутренний угол треугольника, с0 – прилежащий катет, V0 – противоположный катет.
Гипотенузой треугольника скоростей электрона является вектор скорости света в
пространстве электрона cе. Его модуль несколько
превышает c0, а аргумент выражается через угол δ, равный:
![]()
В
показательной форме вектор скорости света электрона может быть представлен так:
![]() , (3)
, (3)
где
аргумент – дополнительный угол.
Столь подробное
обоснование вектора скорости света электрона сe объясняется тем, что в описании ФП света он занимает
центральное место.
Фотон. Излагаемая здесь гипотеза
предполагает, что вектор скорости света фотона сf сдвинут относительно вектора сe в фазовом пространстве на некоторый положительный угол преобразования σt:
![]() .
.
Формально вектор cf может быть получен путем умножения ce (3) на мнимое число i. При этом соотношение между
степовой (поступательной) и спиновой составляющими сохраняются, т. е.
внутренний угол треугольника скоростей не меняется.
На рис. 2 степовая составляющая сst вектора скорости света фотона совпадает с действительной положительной
осью фазовой плоскости, т. к. принято считать с0 действительной величиной.
Косвенным
подтверждением комплексного характера вектора скорости света фотона сf служит явление круговой (циркулярной) поляризации
света в акте элементарного излучения2). Здесь
вектор напряженности электрического поля вращается вокруг направления
распространения света. В светодинамике этому факту сопоставляется вращение
вектора напряженности G-поля.
Взаимное
расположение векторов скорости света электрона сe и фотона сf, показанное на рисунке 2, объясняет неудачные попытки
экспериментаторов разогнать электрон в ускорителе до скорости света так, чтобы
трансформировать его в фотон. Это невозможно – таков результат экспериментов.
Действительно, как следует из рис. 2,
увеличение реальной составляющей до скорости света (V0 ® c0), приводит к существенному
изменению внутреннего угла треугольника скоростей электрона (d ® 45o), но этого недостаточно для
фазового перехода света.
Светодинамика
объясняет недоумение экспериментаторов: для трансформации электрона в фотон, следует
не только разогнать его до скорости c0 в гравитационном поле, но и
раскрутить спираль электрона в ротационном поле. И только после этого –
перевести его в сопряженное пространство, для чего необходим фрактал. Другими
словами, следует повернуть вектор скорости света электрона ce в положительном направлении на угол фазового перехода света st.
При этом наблюдается явление обратного ФП: от электрона – к фотону.
Процесс ФП
света обратим.
Во время прямого ФП света вектор скорости света фотона сf смещается в фазовом пространстве в сторону
отрицательных углов на - st.
Прямой ФП света может быть охарактеризован как лавинообразный процесс свертки
кванта света в GR-поле ядра атома.
Предполагается,
что в процессе свертки вектор скорости света испытывает вращение и кручение в
пространстве так, что образуется спираль света, радиус которой равен
классическому радиусу электрона. На рис. 3
показана траектория движения конца вектора скорости света сf по сходящейся правой логарифмической спирали, в центре которой
расположен фрактал (например, протон). Спираль наложена на фазовую плоскость,
на которой изображено начальное положение вектора сf и его конечное положение (вектор сe) при прямом ФП света. Фазовое рассогласование этих векторов составляет
st.
В процессе перехода вектор скорости с
имеет несколько промежуточных состояний, одно из которых приведено на рисунке.
Физически
описываемый процесс происходит в пространстве GR-поля ядра атома, поэтому
траектория движения фотона может быть изображена пространственной сходящейся
правой логарифмической спиралью. На рис. 4 эта
спираль схематически изображена слева от фрактала. Фрактал разделяет два
сопряженных пространства: света (слева) и массы (справа). Сам фрактал
расположен внутри ядра и представляется центром логарифмических спиралей.
Вторая спираль – это траектория движения элементарной частицы, она является
продолжением первой. Из фрактала обе спирали выглядят совершенно одинаково.
Здесь каждая спираль имеет свое название: световой и массовый порталы
соответственно.
В результате прямого ФП света образуется
микрочастица – свернутый в спираль квант света; гравитационная масса частицы
(масса покоя) определяется энергией кванта, а ее радиус (re) определяет ротационный (магнитный)
«заряд» частицы – положительный или отрицательный, в зависимости от направления
свертки.
Образованная
частица имеет орбитальную V0 и спиновую (с0)
составляющие скорости света, что соответствует спиновой сsp и степовой сst составляющим вектора
скорости света сf.
Фазовый
переход электрона. Свернутый в спираль квант света, теперь уже в качестве микрочастицы,
выбрасывается обратным GR-полем ядра атома на
«поверхность», потенциал которой равен квадрату скорости поступательного движения
электрона:
![]()
Без внешних воздействий на электрон, он движется по орбите радиуса r0 с постоянной скоростью V0 и «сам по себе» совершить обратный фазовый переход не может. Его орбитальный (гравитационный) импульс равен:
рG = mG V0.
Здесь: рG
– импульс орбитального движения, mG – гравитационная масса
электрона, V0 – орбитальная скорость.
Кроме этого,
электрон имеет импульс ротационного поля
рR:
рR = mR с0,
где mR – мнимая масса электрона.
Возможны два типа внешних воздействий на электрон: со стороны налетающей извне частицы (или внешнего поля) и со стороны ядра атома.
Первое
описывается Комптона эффектом. Длина волны электрона в этом случае равна:
![]() ,
,
где lк – комптоновская длина волны
электрона; lе = 2prе – собственная длина волны
электрона; l0 = 2pr0 – длина волны де Бройля.
Радиус орбиты электрона при этом уменьшается до значения (2), что влечет за
собой изменение импульса:
 ,
,
который увеличивается в с0
/ V0 раз и
становится равным:
рк = mGс0. (4)
Точно
такое же значение импульса имеет и фотон, т.е. соблюдается закон сохранения
импульса при трансформации электрона.
Однако равенство
(4) еще не означает, что в Комптона эффекте электрон приобретает скорость света
с0. Дело в том, что комптоновские характеристики электрона: rk, тk, Vk и pk – это обобщенные параметры электрона,
которые присущи электрону всегда, даже в отсутствии внешнего воздействия. Они
остаются неизменными и при ФП электрона.
Между комптоновскими параметрами электрона имеет место равенство:
![]() ,
,
где rk – комптоновский радиус;
![]()
–
комптоновская
масса;
![]() (5)
(5)
–
комптоновская
скорость электрона. В этом случае комптоновский импульс (4) выражается так:
рк = mкVk.
Второй тип
воздействия на электрон выражается в том, что ядро атома возбуждается. Его поле
переходит в нестационарное состояние, возникает GR-индукция. При этом на
потенциальной поверхности атома образуется вихревая GR-воронка, в которую
устремляется электрон. Радиус воронки в ее раскрыве равен радиусу Комптона (2),
а скорость Vk (5).
На рис. 5 изображена вихревая воронка GR-поля
возбужденного атома, имеющая форму пространственной сходящейся спирали, высота
которой равна радиусу орбиты r0, а наименьший радиус равен rе; он связывается с радиусом ядра атома.
GR-воронка повторяет форму известного атмосферного вихря – торнадо и
отражает структуру нестационарного поля ядра. Векторы напряженности
индуцированных G и R-полей вращаются по
сходящимся спиральным траекториям, увлекая электрон к ядру атома.
Существует
несколько путей для описания фазового перехода. Например, с помощью клотоиды3) – кривой, для которой радиус
кривизны обратно пропорционален длине дуги. Для этого следует преобразовать
выражение (2) в зависимость:
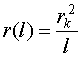 ,
,
где r –
радиус кривизны электрона, l – длина дуги спирали по рис. 5. Подобное описание ФП электрона полезно
тем, что наглядно показывает: фотон есть кососимметричное отражение электрона.
Кроме того, оно выявляет, что сопряженные пространства фотона и электрона,
видимо, отличается знаком кривизны.
Ниже излагается способ описания трансформации
электрона в фотон, основанный на постоянстве комптоновских характеристик
электрона: rk, pk, Vk и mk. Он состоит в рассмотрении процесса движения конца вектора скорости
света с на фазовой плоскости из своего начального положения сe, в конечное положение – сf. На рис. 6 фазовая траектория
вектора c изображена множеством точек в интервале 1-2 и пунктирной линией в
интервале 2-3. Направление движения конца вектора обозначено стрелками.
Геометрическим местом множества точек в интервале 1-2 является кривая обратной
зависимости между составляющими сR и сG
вектора с.
Смещение
вектора скорости света имеет место в интервале 1-2 фазового перехода. Этому участку
соответствует движение конца вектора сe по логарифмической спирали (рис. 3) на
фазовой плоскости в сторону увеличения угла (против часовой стрелки). Этому же
процессу сопоставляется движение электрона по спирали (рис. 5) вихревой GR-воронки возбужденного атома
в направлении ядра атома. Тот же процесс отображается на рис. 4 в виде движения электрона e по
сходящейся спирали в направлении фрактала.
При каждом
обороте электрона по пространственной спирали рис.4
и рис. 5, вектор света с (рис. 6) поворачивается на угол +d, что обеспечивает его
скачкообразное перемещение по кривой 1-2. Каждый скачок вектора с
отражается точкой на фазовой траектории рис. 6,
так что образуется множество промежуточных состояний вектора света.
По мере
приближения электрона к ядру атома, его поступательная скорость растет, радиус
«кружков Лармора» уменьшается. Ввиду постоянства Vk (5), спиновая составляющая
скорости уменьшается. Радиус самой частицы увеличивается из-за постоянства rk (2). За счет обратного вращения GR-воронки, ротационное поле
электрона слабеет, а гравитационное – усиливается: энергия R-поля
электрона «перетекает» в G- поле.
Наконец, на
расстоянии rе от центра ядра, поступательная скорость
электрона достигает скорости света с0, а мнимая (ротационная)
составляющая уменьшается до значения V0. При этом радиус самой
частицы становится равным r0 (радиус орбиты).
К этому моменту
вектор скорости света с попадает в точку 2 на фазовой плоскости рис.6; в этом случае он равен:
с = с0 – iV0.
Второй этап
прямого ФП света (интервал 2-3) заключается в скачкообразном перемещении
вектора скорости света с в сопряженное пространство, что
соответствует увеличению фазы на угол 2d (против часовой стрелки).
При этом он пересекает действительную ось системы координат, разделяющую
сопряженные векторы ![]() и сf. Вектор скорости с приходит к своему конечному состоянию
ФП (вектору скорости фотона):
и сf. Вектор скорости с приходит к своему конечному состоянию
ФП (вектору скорости фотона):
сf = с0 + iV0.
Физически этот
этап ФП света состоит в том, что «электрон» со скоростью света проходит ядро атома (рис.
5) или фрактал по рис. 4, что то же самое.
Слово «электрон» взято в кавычки, т. к. фактически электроном (и фотоном)
называется конечное состояние света при ФП. Между этими двумя крайними
состояниями, «внутри» ФП, находится световая энергия или просто – свет.
Поскольку
смещение вектора скорости света с при каждом обороте спирали
составляет угол d, можно вычислить количество
оборотов спирали:
 ,
,
что соответствует смещению
на угол трансформации:
st = 2pn =
430,5p рад.
В заключение
следует отметить, что фазовая картина прямого ФП света несколько отличается от рассмотренной
выше, но только формой. По содержанию – это обратный процесс, что отражено на рис. 7.
Выводы:
1.
Светодинамика
позволяет решать задачи, ранее недоступные науке.
2.
Система
уравнений Максвелла для GR-поля является теорией
динамики света.
© г. Сочи, 2001г.