Р. Вишневский
Светодинамика электрона.
В статье
выяснено конкретное значение гравитационного потенциала на орбите электрона в
атоме водорода; определено, что понятие «элементарный электрический заряд» –
абсурдно; уточнено место электромагнетизма в светодинамике.
Установлено, что ньютоновское понятие гравитационной массы должно быть дополнено мнимой, безынерционной составляющей.
Одной из задач светодинамики является выражение именных единиц физических величин электромагнетизма в единицах гравитационной системы. И основным здесь оказывается вопрос соотношения между единицами длины и времени, принятого в электродинамике.
Физической величиной, выражающей в светодинамике это соотношение, является т. н. поток напряженности гравитационного поля
![]() .
.
Здесь: G – напряженность гравитационного поля, S – замкнутая поверхность, внутри которой находится масса т, создающая G-поле. При этом поток напряженности выражается теоремой Остроградского – Гаусса для гравиротационного (GR) поля:
 ,
,
где γ – гравитационная постоянная для данного пространства. (Здесь и ниже используется система СИ).
Соответствующее выражение для потока напряженности электрического поля не дает явного значения потока:
 ;
;
т. к. в размерности Ne присутствует неопределенное отношение кг/Кл.
В рамках замкнутой системы именных единиц электродинамики решить вопрос об отношении единиц длины и времени невозможно. Вся система основана на электрическом заряде и его единице – кулоне. Поэтому определение значения последнего в единицах массы – килограммах – непосредственно связано с выяснением фактического значения потока напряженности G-поля.
Решению этого вопроса посвящена данная статья.
Гравитационный потенциал, создаваемый массой т, связан с потоком напряженности G-поля так:
 ,
,
где φG – отрицательная скалярная величина, гравитационный потенциал на расстоянии r от источника потока, массы т.
С другой стороны известно, что гравитационный потенциал поля равен квадрату вектора скорости V движущегося тела (частицы):
![]() ,
,
т. ч. для определения G-потенциала протона на орбите электрона в атоме водорода, например, достаточно найти модуль его скорости движения вдоль орбиты.
Следует заметить, что современная наука описывает электрон с помощью волновой функции, но от этого он еще не потерял свойств частицы, с которой может быть связан вектор скорости.
Возможность определения модуля вектора скорости частицы предоставляет формула де Бройля:
![]() ,
,
где λБ – длина волны де Бройля, т – масса движущейся со скоростью V частицы, h – постоянная Планка. В случае невозбужденного атома водорода длина волны де Бройля λБ равна длине боровской орбиты электрона:
![]() ;
;
r1 = 5,2917706·10-11 м – радиус боровский первый. Массой т в данном случае является масса покоя электрона т0 = 9,1095345·10-31 кг.
Итак, скорость движения электрона вдоль первой боровской орбиты составляет:
 ,
,
следовательно, гравитационный потенциал ядра атома водорода на первой боровской орбите по абсолютной величине равен:
 . (1)
. (1)
На вопрос: возможна ли подмена электрического потенциала гравитационным, светодинамика отвечает положительно: это поле еще долго можно называть кулоновским, а потенциал – электрическим, но нельзя отрицать очевидный факт – если материальная частица движется, то имеется и гравитационный потенциал поля, в котором она движется, и это поле – гравитационное.
Возможно, что описанный способ вычисления гравитационного потенциала на боровской орбите покажется читателю не вполне убедительным, поэтому ниже предлагается другой путь определения той же физической величины. Он несколько сложнее первого, но основан на безукоризненных данных – сериях спектральных линий атома водорода.
Элементарный электрический заряд. Допущение о том, что потенциал кулоновского поля равен гравитационному является очень серьезным ограничением э/м системы. Фактически это означает: электрический заряд электрона является массой, а кулоновское поле – полем тяготения электрона.
Действительно, из равенства
![]()
на боровской орбите атома водорода следует:
 ,
(10)
,
(10)
единица заряда:
![]()
и, наконец, значение элементарного электрического заряда в G-системе:
![]() (11)
(11)
Этот результат свидетельствует о том, что гравитационное поле электрона образует его масса покоя. Но для полной характеристики электрона этого недостаточно.
Комплексная масса электрона. Светодинамика является теорией гравиротационного (GR) поля, что по сути дела, означает обобщение электрического поля до уровня гравитации. Соответственно магнитное поле обобщается до ротационного (R-поля).
Основным законом светодинамики считается т. н. система уравнений Максвелла для GR-поля. В дифференциальной форме это:
 (12)
(12)
Здесь: G и D – векторы напряженности и смещения (индукции) гравитационного поля соответственно; R и Ω – векторы напряженности и индукции ротационного поля; ρт – объемная плотность массы; jm – вектор плотности тока массы.
Для макромира вводятся абсолютные: гравитационная γ0 и ротационная χ0 в рационализированной форме:
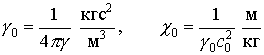 .
.
где γ = 6,672·10-11
Н·м2кг-2
– гравитационная постоянная, ![]() – потенциал предельной
скорости света.
– потенциал предельной
скорости света.
Подробное описание GR-поля содержится в другой работе автора2).
Собственно электрон светодинамика рассматривает как GR-систему нестационарного гравиротационного поля. При этом имеет место явление GR-индукции. Система описывается уравнениями (12); гравитационная постоянная γе существенно отличается от абсолютной гравитационной γ0 (в этом «повинен» сам электрон) и характеризует пространство электрона.
Ниже приводится описание GR-системы электрона в стационарном состоянии путем характеристики G- и R-полей электрона с помощью понятия массы.
G-поле электрона характеризует масса покоя электрона т0. Это ньютоновская инертная масса, действительная часть комплексной массы электрона.
R-поле электрона характеризуется мнимой массой. Эта масса безынерционна, она ответственна за гироскопическую силу. Мнимая часть массы электрона вводится так: предполагается, что на расстоянии классического радиуса rе от центра электрона со скоростью света с0 распространяется волна, длина которой
![]() .
.
Она называется собственной длиной волны электрона и создает мнимую часть его массы:
 .
.
Эту массу электрона не следует отождествлять с зарядом электрона е, т. к. она
характеризует ротационное (магнитное) поле электрона, а е – заряд электрический. Однако двусмысленность понятия «заряд» сохраняется.
С учетом действительной части массы электрона
![]()
и отрицательного знака заряда, комплексная масса электрона равна:
![]() .
(13)
.
(13)
Модуль массы
![]() ,
,
аргумент
![]() .
.
Ниже приводятся некоторые физические величины, вычисленные с помощью комплексной массы электрона (13).
Гравитационная
постоянная пространства электрона γе
определяется из выражения для потенциала самого электрона (![]() ):
):
 .
.
Кулона закон (r = 1 м) выражается так:
 .
.
Здесь мнимая часть составляет гироскопическую силу, а действительную часть (кулоновскую силу) создает гравитационная масса электрона т0.
Постоянная тонкой структуры:
 .
.
Радиус орбиты первой боровской:
 .
.
Собственная энергия электрона:
![]() .
.
Мнимая часть энергии при «аннигиляции» электрона не излучается, она принадлежит фотону.
Ротационный момент электрона. Одним из значительных достижений квантовой электродинамики считается вычисление аномального магнитного момента электрона с помощью «вакуумных добавок».
Светодинамика эту задачу решает легко, причем комплексно. Аналогом магнитного момента в данном случае является ротационный (R) момент комплексной массы электрона. Соответственно G-момент последнего соответствует механическому моменту электродинамики.
1. Ротационный момент Бора вычисляется по известной формуле, где в качестве заряда е выступает мнимая масса электрона:
 .
.
2. Орбитальный комплексный момент электрона:
![]() .
.
Здесь действительная часть составляет орбитальный гравитационный момент электрона
![]() .
.
Мнимая часть является орбитальным ротационным моментом электрона и равна:
![]() .
.
3. Спиновый комплексный момент электрона выражается равенством:
![]() .
.
Здесь спиновый гравитационный момент (![]() ) электрона (действительная часть) ничтожен по
сравнению со спиновым ротационным моментом, равным:
) электрона (действительная часть) ничтожен по
сравнению со спиновым ротационным моментом, равным:
![]() .
.
Следует
заметить: электродинамика полагает, что спиновый
ротационный момент в е/т раз превосходит спин электрона (![]() ) и это верно. Но то, что спиновый
ротационный момент равен магнетону Бора, - ошибка.
) и это верно. Но то, что спиновый
ротационный момент равен магнетону Бора, - ошибка.
4. Полный ротационный момент электрона вычисляется так;
 .
.
Этот результат уступает по точности упомянутому выше, зато получен без помощи «вакуума».
Приведенные примеры вычисления некоторых характеристик электрона ясно показывают, что электродинамика пользуется, по сути дела, проекциями вектора массы электрона. В таком случае понятие «электрический заряд» не отражает сущности электрона. Мнимая масса электрона – это магнитный монополь электрона. В светодинамике он называется ротатор света.
С другой стороны, светодинамика логична и последовательна в описании электрона, а потому является законной правопреемницей электродинамики. Это – новый уровень познания природы.
В заключение следует заметить, что численное значение потока напряженности G-поля электрона
 .
.
представляет собой действительную величину и с большой точностью совпадает с аналогичным потоком протона (9), что предполагает равенство по абсолютной величине их мнимых масс. Поэтому комплексную массу протона следует записать так:
![]() .
.
Соотношение действительной и мнимой частей массы протона
![]() ,
,
тогда как для электрона эта константа составляет
 .
.
Выводы. 1. Светодинамика обобщает электромагнетизм до гравиротационного (GR) поля. Она в состоянии описывать все известные взаимодействия микро- и макромира на основе системы уравнений Максвелла для GR-поля.
2. Из них непосредственно следует факт существования в природе ротационного поля. Модуль вектора ротационной индукции получен Кеплером в третьем законе движения планет Солнечной системы:
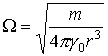 .
.
3. Ньютоновское понятие инертной массы следует дополнить понятием мнимой массы.
4. Понятие «элементарный электрический заряд» е абсурдно, т. к. исключая «электрическую» часть массы электрона т0, оно ставит знак равенства между е и магнитным монополем электрона.
© г. СОЧИ 2001 г.